轉子動力學建模分析
發布時間:
2024-07-03 17:37
轉子材料的不均勻、制造誤差、結構的不對稱等諸因素導致轉子在旋轉時會產生離心慣性力組成一個空間力系,使轉子動不平衡。當試件上有不平衡質量存在時,試件以角速度ω轉動后產生離心慣性力 F = mrω2,它可以分成垂直分力Fy和水平分力 Fx,由于平衡機的工字型板簧和擺架在水平方向(繞 y 軸)抗彎剛度很大,所以水平分力 Fx 對擺架的振動影響很小可忽略不計。而在垂直方向上(繞 x 軸)的抗彎剛度小,因此在垂直分力產生的力矩的作用下,使擺架產生周期性的上下振動。因此,動平衡機可簡化為自由度為2的線性受迫振動系統。設轉子質量為 M ,對過質心且垂直于紙面的軸的轉動慣量為 J,不平衡量的質量分別為 m1、m2,板簧和彈簧勁度系數分別為k1、k2,轉子與不平衡量的相對位置如圖 1 所示。
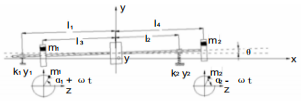
圖 1 轉子-支撐振動系統動力學模型
設初始狀態時系統水平,過質心建立坐標系。在運動的某一時刻,轉子質心沿 y 軸方向的位移為 y,轉角為 θ,板簧相對于初始位置的伸長量分別為 y 1、y 2。可得轉子運動微分方程:
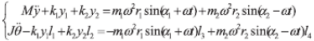 (1)
(1)
式 1 中
r1—— m1 距回轉中心的半徑
r2—— m2 距回轉中心的半徑
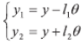 (2)
(2)
將 2 式代入 1 式整理可得 3 式
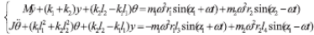 (3)
(3)
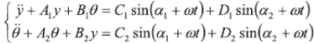 (4)
(4)
式 4 中
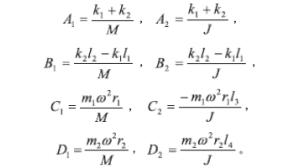
1)解方程組 4 所對應的齊次方程組,可得 y與 θ的 固 有 角 頻 率 p1、p2 均 為 方 程 p4 - ( A1 +A2)p2 + A 1A 2 - B1B2 = 0 的兩正根:
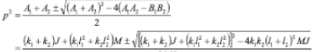 (5)
(5)
由式 5 可知,動平衡實驗機振動系統的固有頻率和 M 、k 1、k 2、m1、 m2、J 參數有關。
2)令轉子質心位移 y 和轉角 θ如式 6、7 所示。
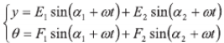 (6)
(6)
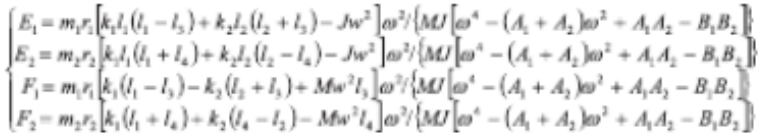 (7)
(7)
代入原方程組可解得轉子質心位移 y 和轉角 θ的一組特解:
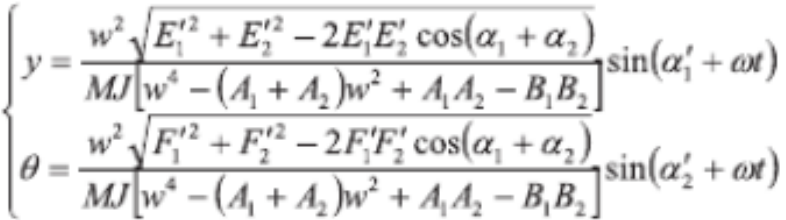 (08)
(08)
其中, α1′和 α2′為相關常數,式中
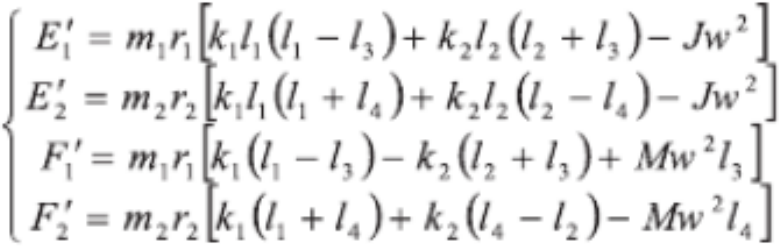
相關新聞
2024-07-03
平衡機發展迄今已經有一百多年的歷史。1866年,德國西門子公司發明了發電機。4年后,加拿大人Henry Martinson申請了平衡技術的專li ,拉開了平衡校正產業的序幕。
2024-07-03
電機轉子裝配工的一般操作規程如下: 1、工作前,整理場地,放穩各零、部件,并檢查裝配使用工具和工作環境是否安全良好。 2、吊放電機機座、底板、定子、轉子、軸承等大型部件時必須放好方箱或墊木...


